تابع یکی از مفاهیم نظریه مجموعهها و حساب دیفرانسیل و انتگرال است. بطور ساده میتوان گفت که به قاعدههای تناظری که به هر ورودی خود یک و فقط یک خروجی نسبت میدهند، تابع گفته میشود.

نمودار تابع
![\begin{align}&\scriptstyle f \colon [-1,1.5] \to [-1,1.5] \\ &\textstyle x \mapsto \frac{(4x^3-6x^2+1)\sqrt{x+1}}{3-x}\end{align}](http://upload.wikimedia.org/wikipedia/fa/math/5/5/e/55ecbb104124c17699f758a715f2b6a5.png)
پیشینه
تابع به عنوان مفهومی در ریاضیات، توسط گوتفرید لایبنیتس در سال ۱۶۹۴، با هدف توصیف یک کمیت در رابطه با یک منحنی مانند شیب یک نمودار در یک نقطه خاص به وجود آمد. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم.
واژه تابع بعدها توسط لئونارد اویلر در قرن هجدهم، برای توصیف یک گزاره یا فرمول شامل متغیرهای گوناگون مورد استفاده قرار گرفت، مانند f(x) = sin(x) + x3.
در طی قرن نوزدهم، ریاضیدانان شروع به فرمول بندی تمام شاخههای ریاضی براساس نظریه مجموعهها کردند. وایراشتراس بیشتر خواهان به وجود آمدن حساب دیفرانسیل و انتگرال در علم حساب بود تا در هندسه، یعنی بیشتر طرفدار تعریف اویلر بود.
در ابتدا، ایده تابع ترجیحاً محدود شد. ژوزف فوریه مدعی بود که تمام توابع از سری فوریه پیروی میکنند در حالی که امروزه با گسترش تعریف توابع، ریاضیدانان توانستند به مطالعه توابعی در ریاضی بپردازند که که در سراسر دامنه خود پیوسته ولی در هیچ نقطهای مشتقپذیر نیستند این گونه توابع توسط وایراشتراس معرفی شدند. کشف چنین توابعی موجب شد تا توابع تنها به توابع پیوسته و مشتقپذیر محدود نشوند.
تا انتهای قرن نوزدهم ریاضیدانان در هر موضوع ریاضی به دنبال تعریفی بودند که براساس نظریه مجموعهها و نتایج آن باشد. دیریکله و لوباچوسکی هر یک به طور مستقل همزمان تعریف «رسمی» از تابع ارائه دادند.
بر طبق این تعریف، تابع حالت خاصی از یک رابطه است که در آن برای هر مقدار اولیه یک مقدار ثانویه منحصر به فرد وجود دارد.
تعریف تابع در علم رایانه، به عنوان حالت خاصی از یک رابطه، به طور گستردهتر در منطق و علم تئوری رایانه مطالعه میشود.
در دیگر علوم
توابع در شاخههای مختلف علوم کاربرد فراوان دارند. برای مثال در فیزیک، هنگامی که میخواهیم رابطه بین چند متغیر را بیان کنیم، مخصوصاً هنگامی که مقدار یک متغیر کاملاً وابسته به متغیرهای دیگر است از توابع استفاده میشود.
توابع در علوم مختلف بیشتر به عنوان عملگر در نظر گرفته میشوند که کاری را بر روی ورودیهای خود انجام میدهند. توابع را همچنین مورد استفاده در علم رایانه برای مدلسازی ساختمان دادهها و تأثیرات الگوریتم میبینیم.
تعریف تابع
تابع را میتوان به عنوان قاعدهای خاص برای تناظر بین اعضای دو مجموعهٔ دامنه و برد تعریف کرد. به بیان دقیقتر، اگر A و B دو مجموعه باشند، یک تابع از مجموعهٔ A به مجموعهٔ B را میتوان قاعدهای تعریف کرد که به هر عضو مجموعه A چون a، یک و فقط یک عضو از مجموعه B را چون f(a) نسبت میدهد. تابع f از مجموعه A به مجموعه B را با 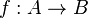 نشان میدهیم.
نشان میدهیم.

شکل ۱. نمونهای از یک تناظر که تابع نیست
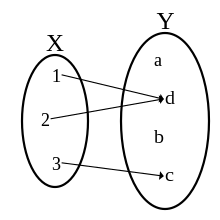
شکل ۲. نمونهای از یک تابع
برای نمونه تناظر شکل ۱ نمایش دهنده یک تابع نمیباشد. چراکه عضو ۳ از مجموعه X به دو عضو (b و c) از Y متناظر شدهاست. اما شکل ۲ نشان دهنده یک تابع است. هر چند که دو عضو گوناگون از مجموعه X به یک عضو خاص از Y نسبت داده شدهاند.
تابع f به عنوان هنجار تناظر، چیزی بجز توصیف نحوه تناظر اعضای A به B نیست که به طور کامل بهوسیله همه زوجهای مرتب (a,f(a)) برای هر 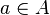 مشخص میشود پس تابع f را میتوان به عنوان مجموعه همه این زوجهای مرتب، یعنی مجموعه همه زوجهای مرتبی که مولفه اول آنها عضو A بوده و مولفه دوم آنها تصویر مولفه اول تحت تابع f در Y است، تعریف کرد. شرط تابع بودن تضمین میکند که هیچ دو زوج متمایزی در تابعf دارای مولفه اول یکسان نخواهند بود.
مشخص میشود پس تابع f را میتوان به عنوان مجموعه همه این زوجهای مرتب، یعنی مجموعه همه زوجهای مرتبی که مولفه اول آنها عضو A بوده و مولفه دوم آنها تصویر مولفه اول تحت تابع f در Y است، تعریف کرد. شرط تابع بودن تضمین میکند که هیچ دو زوج متمایزی در تابعf دارای مولفه اول یکسان نخواهند بود.
در این صورت در تابع 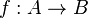 برای هر
برای هر 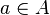 گزاره
گزاره 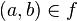 را به صورت b = f(a) نشان میدهیم.
را به صورت b = f(a) نشان میدهیم.
تعریف دقیق
یک تابع از مجموعه X به مجموعه Y رابطهای چون f از مجموعه X به مجموعه Y است که دارای شرایط زیر باشد:
- دامنه f مجموعه X باشد، یعنی domf = X.
- برای هر
 عنصر یگانه
عنصر یگانه 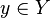 موجود باشد که (x,y)inf یا به عبارتی هیچ دو زوج مرتب متمایزی متعلق به f دارای مولفه اول یکسان نباشند. شرط یگانگی را به طور صریح میتوان یه این صورت فرمول بندی کرد که اگر
موجود باشد که (x,y)inf یا به عبارتی هیچ دو زوج مرتب متمایزی متعلق به f دارای مولفه اول یکسان نباشند. شرط یگانگی را به طور صریح میتوان یه این صورت فرمول بندی کرد که اگر 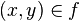 و
و  آنگاه الزاماً y = z.
آنگاه الزاماً y = z.
علامتها
برای هر  یگانه عضو y در Y که به ازای آن
یگانه عضو y در Y که به ازای آن 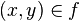 را با f(x) نشان میدهیم. در مورد تابع این علامتگذاری، سایر علامتگذاریهایی را که در مورد روابط کلی تر استفاده میشوند چون
را با f(x) نشان میدهیم. در مورد تابع این علامتگذاری، سایر علامتگذاریهایی را که در مورد روابط کلی تر استفاده میشوند چون 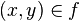 یا xfy را متروک ساختهاست. از این پس اگر f یک تابع باشد، بجای
یا xfy را متروک ساختهاست. از این پس اگر f یک تابع باشد، بجای 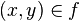 یا xfy مینویسیمy = f(x). عضو y را مقدار تابع به ازای متغیر یا شناسه x یا تصویر x تحت f میگوییم و نیز x را پیش نگاره y میگوییم.
یا xfy مینویسیمy = f(x). عضو y را مقدار تابع به ازای متغیر یا شناسه x یا تصویر x تحت f میگوییم و نیز x را پیش نگاره y میگوییم.
اگر f تابعی از مجموعه X به (در یا به توی) مجموعه Y باشد، این مطلب را به صورت سه تایی (f,X,Y) یا به طور معمول تر برای توابع با 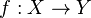 نشان میدهیم.
نشان میدهیم.
مشخص کردن تابع
برای مشخص کردن یک تابع باید دامنه و ضابطه آن را بشناسیم. منظور از ضابطه یک تابع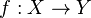 ، فرمول و یا دستوری است که برطبق آن برای هر
، فرمول و یا دستوری است که برطبق آن برای هر  ، مقدار تابع f در x یعنی f(x) تعیین میشود. ضابطه تابع را میتوان به صورت یک گزاره جبری، مجموعهای از زوجهای مرتب یا یک رابطه بازگشتی مشخص کرد.
، مقدار تابع f در x یعنی f(x) تعیین میشود. ضابطه تابع را میتوان به صورت یک گزاره جبری، مجموعهای از زوجهای مرتب یا یک رابطه بازگشتی مشخص کرد.
به این ترتیب برای مشخص کردن یک تابع از مجموعه X به مجموعه Y مینویسیم 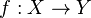 و سپس ضابطه آن را ذکر میکنیم.
و سپس ضابطه آن را ذکر میکنیم.
در مواقعی که بیم ابهام نرود دامنه تابع ذکر نشده و به ذکر ضابطه تابع بسنده میشود. مثلاً عرف بر این است که در حساب دیفرانسیل و انتگرال دامنه توابع در صورت ذکر نشدن اعداد حقیقی یا بازهای از اعداد حقیقی باشد.
برای نمایش بهتر، تابع را که خود یک هنجار (قاعده) برای تناظر است با f نشان میدهیم و ورودی یا شناسهٔ این تابع را باx نشان میدهیم که ممکن است عدد هم نباشد. یگانه مقدار خروجی که هنجار f به ورودی x نسبت میدهد را بجای y اینبار با f(x) نشان میدهیم و آن را مقدار تابع f در x یا تصویر x تحت f میگوییم. همچنین از این پس به قاعدهای که هر x را به y = f(x) نسبت میدهد ضابطه تابع میگوییم.
نباید تابع را با ضابطهٔ آن اشتباه کرد. به عنوان مثال در مثال بالا f معرف خود تابع و گزاره f(x) معرف ضابطه تابع است.
دامنه و برد تابع
یک تابع f از مجموعه X به توی مجموعه Y را به عنوان نوعی رابطه از مجموعه X به Y تعریف کردیم. مفاهیم دامنه (تابع) و برد همانگونه که برای روابط در حالت کلی قابل تعریفاند، به طریق اولی برای تابع f نیز قابل تعریف خواهند بود. بنا به تعریف دامنه تابع f که با domf نموده میشود، همان مجموعه X است. برد تابع f نیز مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند. برد تابع f را با ranf یا Imf نشان میدهیم. بنابه تعریف داریم:
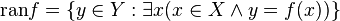
اما همانطور که در گذشته نیز اشاره شد و از تعریف فوق نیز قابل برداشت است، برد f در حالت کلی لزوماً برابر مجموعه Y نمیباشد بلکه زیرمجموعهای از آن است. برای تمایز بین مجموعه Y و برد تابع f به مجموعه Y همدامنه تابع f میگویند و آن را با codomf نشان میدهیم و بنا بر آنچه گفته شد، برد تابع زیرمجموعهای از همدامنهاش هست.
به عنوان مثال فرض کنید {X={۱٬۲٬۳ و {Y={a,b,c,d و تابع f:X→Y به صورت {(f={(۱,a),(۲,b),(۳,c تعریف شده باشد. وضوحاً دامنه این تابع مجموعه X است(میتوان برای تعیین آن مجموعه همه مولفههای اول زوجهای مرتب f را در نظر گرفت) ولی برد آن بنابه تعریف مجموعه {a,b,c} است که آشکارا زیرمجموعه حقیقی Y است.(یعنی زیرمجموعه آن است ولی با آن برابر نمیباشد)
در حقیقت برد تابع f مجموعه همه مولفههای دوم زوج مرتبهای f است. مجموعه همه عناصری از Y که به ازای یکx∈X داشته باشیم (y=f(x.
تساوی دو تابع
فرض کنید f:X→Y و g:Z→W دو تابع باشند. در این صورت تساوی f=g، تساوی بین دو مجموعه است و لذا f=g اگر و فقط اگر اعضای f و g یکسان باشند. یا به عبارتی دو تابع f و g با هم برابرند اگر و تنها اگر دامنهشان با هم برابر باشد و برای هر x از دامنه مشترکشان، (f(x)=g(x.
تحدید و توسیع
فرض کنید f:X→Y یک تابع و A زیرمجموعهای از X باشد. در این صورت یک روش برای ساختن تابعی چون g از مجموعه A به مجموعه Y این است که برای هر g(x)، x∈A را مساوی (f(x تعریف کنیم. یعنی تابع g:A→Y با ضابطه (g(x)=f(x. بر خوانندهاست که خوش تعریفی این تابع را تحقیق کند. ممکن است راه دیگری نیز برای بیان این مطلب بیابیم و آن این است که دامنه تابع f را به زیرمجموعه A از X تقلیل دهیم. در این صورت تابعی خواهیم داشت که این بار نه بر روی همه اعضای X بلکه فقط بر روی عناصر زیرمجموعه خاصی از X یعنی A اثر میکند و لذا دامنه آن از X به A تغییر مییابد. چنین تابعی را که همان g است تحدید تابع f به مجموعه A میگوییم و آن را با f|A یا f|A نشان میدهیم. با این نمادگذاری داریم g=f|A. همچنین تابع f را توسیع تابع g به مجموعه X میگوییم.
بنابراین مفاهیم تحدید و توسیع دو مفهوم متقابل به هم میباشند. تحدید یک تابع به زیرمجموعهای از دامنه خود همواره یک تابع است اما توسیع دامنه یک تابع به یک مجموعه جدید که دامنه تابع قبل زیرمجموعهای از آن است همواره تابع نمیباشد ولذا در مورد توسیع توابع احتیاط بیشتری لازم است. به طور کلی اگر f:A→Y یک تابع باشد توسیع تابع f به مجموعه X تابعی چون g با دامنه X است، به طوری که تحدید g به مجموعه A برابر تابع f باشد یعنی g|A=f.
هچنین میتوان همدامنه یک تابع را نیز تحدید کرد البته در این کار احتیاط لازم است، چراکه نباید اعضایی را که متعلق به برد تابع است را حذف نمود. اما اگر f:X→Y یک تابع باشد، با تحدید Y به (f(X که همان برد تابع f است میتوان تابع (f:X→f(X را تشکیل داد که پوشا نیز هست.
تصویر و تصویر معکوس
اگر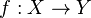 یک تابع و A زیرمجموعهای از X باشد، ممکن است بخواهیم مجوعهای را در نظر بگیریم که عناصر آن تصویر عناصر A تحت f میباشند. یعنی مجموعهای که از تأثیر تابع f روی هر عضو مجموعه A حاصل میشود. چنین مجموعهای را تصویر یا نگاره A تحت تابع f میگوییم و آن را با f(A) نشان میدهیم و به این صورت تعریف میکنیم:
یک تابع و A زیرمجموعهای از X باشد، ممکن است بخواهیم مجوعهای را در نظر بگیریم که عناصر آن تصویر عناصر A تحت f میباشند. یعنی مجموعهای که از تأثیر تابع f روی هر عضو مجموعه A حاصل میشود. چنین مجموعهای را تصویر یا نگاره A تحت تابع f میگوییم و آن را با f(A) نشان میدهیم و به این صورت تعریف میکنیم:
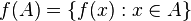
بنابر این (y \to f(A اگر و فقط اگر به ازای y = f(x)، 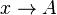 یا به بیان نمادین:
یا به بیان نمادین:
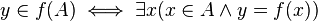
به عنوان مثال اگر X = {1,2,3,4,5} و Y = {a,b,c,d,e} و 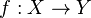 به صورت:
به صورت:
- f = {(1,a),(2,b),(3,c),(4,d),(5,d)}
تعریف شود و زیرمجموعه A از X به صورت A = {1,3,4}در نظر گرفته شود در این صورت:
- f(A) = {f(1),f(3),f(4)} = {a,c,d}
حال چونX نیز زیرمجموعهای از خودش است میتوان f(X) را نیز تشکیل داد، که در این صورت بنا به تعریف داریم:
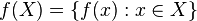
که عبارت است از مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند که بنابه تعریف همان برد تابع f یعنی ranf است. به این ترتیب برد f را میتوان تصویر X تحت تابع f تعریف کرد.
اجتماع توابع-توابع چند ضابطهای
بسیار اتفاق میافتند که مقدار یک تابع در سراسر دامنهاش با یک ضابطه مشخص نمیشود مثلاً ممکن است دامنه تابع f که آن را X مینامیم را به n مجموعه X۱,X۲,X۳,...,Xn افراز کنیم و تابع f با دامنه X را برای هر x∈Xi به صورت (f(x)=fi(x تعریف کنیم که در آن fi تابعی با دامنه Xi است. همچنین در این صورت میتوان تابع f را برای هر x از دامنه به صورت زیر نوشت:
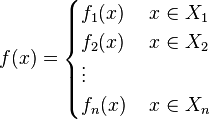
در این صورت f را تابعی با n ضابطه میگوییم.
در مثالی دیگر فرض کنید f:X→Y و g:Z→W دو تابع باشند که برای هر x متعلق به اشتراک X و Y (اشتراک دامنه f,g) داشته باشیم (f(x)=g(x. در این صورت تابع  اجتماع دو تابع f,g را به صورت زیر تعریف میکنیم:
اجتماع دو تابع f,g را به صورت زیر تعریف میکنیم:
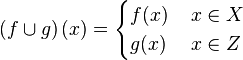
برخوانندهاست که خوش تعریفی این تابع را تحقیق کند. این مفهوم را میتوان گسترش داد یعنی اگر 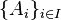 خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i∈I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i∈I را با دامنه
خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i∈I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i∈I را با دامنه 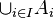 را به صورت برای هر x از دامنه به صورت
را به صورت برای هر x از دامنه به صورت
(f(x)=fi(x اگر x∈Ai تعریف کرد. در ادامه نمونههایی از توابع چند ضابطهای را خواهید دید.
نمودار تابع

شکل ۳. نمودار پیکانی یک تابع
منظور از نمودار یک تابع 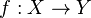 به تصویر کشیدن تناظری است که f بین دو مجموعه X و Y ایجاد میکند. برای این کار برای همه روابط و بلاخص توابع عموماً از نمودار پیکانی استفاده میشود. برای رسم نمودار پیکانی تابع
به تصویر کشیدن تناظری است که f بین دو مجموعه X و Y ایجاد میکند. برای این کار برای همه روابط و بلاخص توابع عموماً از نمودار پیکانی استفاده میشود. برای رسم نمودار پیکانی تابع 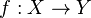 ، دو منحنی بسته نظیر آنچه در نمودار ون استفاده میشود را برای نمایش مجموعه X و Y انتخاب میکنیم و عناصر هر یک را بهوسیله نقاطی در آنها مشخص میکنیم. سپس بین هر عضو
، دو منحنی بسته نظیر آنچه در نمودار ون استفاده میشود را برای نمایش مجموعه X و Y انتخاب میکنیم و عناصر هر یک را بهوسیله نقاطی در آنها مشخص میکنیم. سپس بین هر عضو  و (f(x یک پیکان از x به (f(x به نشانه تناظر بین آن دو رسم میکنیم. به عنوان مثال اگر {X={۱٬۲٬۳٬۴٬۵ و {Y={a,b,c,d,e و
و (f(x یک پیکان از x به (f(x به نشانه تناظر بین آن دو رسم میکنیم. به عنوان مثال اگر {X={۱٬۲٬۳٬۴٬۵ و {Y={a,b,c,d,e و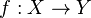 به صورت f = {(1,a),(2,b),(3,c),(4,d),(5,d} تعریف شده باشد نمودار پیکانی آن به صورت مقابل است.
به صورت f = {(1,a),(2,b),(3,c),(4,d),(5,d} تعریف شده باشد نمودار پیکانی آن به صورت مقابل است.

شکل ۴. نمونهای از نمودار یک تابع حقیقی در دستگاه مختصات دکارتی
این روش گرچه مناسب است ولی برای نمایش همه توابع بویژه توابعی با دامنه اعداد حقیقی (و به طور کلی توابعی که عددی هستند) چندان کاربرد ندارد. اگر f تابعی با دامنه اعداد حقیقی R باشد آن را تابع حقیقی میگوییم و برای نمایش نمودار آن از دستگاه مختصات دکارتی استفاده میکنیم. روش کار به این صورت است که برای هر 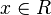 زوج مرتب ((x,f(x) که نماینده نقطهای در صفحه دکارتی است را رسم میکنیم و به این ترتیب نمودار تابع f حاصل میشود. رسم نمودار تابع، باعث میشود دیدی کلی نسبت به آن تابع پیدا کنیم و همچنین بسیاری از خواص مربوط به توابع بویژه توابع حقیقی، مانند پیوستگی، مشتق پذیری، نقاط بحرانی و عطف، صعودی یا نزولی بودن و... از روی نمودار آنها قابل تعیین است. به عنوان مثال با بررسی شکل (۴) میتوان گفت این تابع در چه بازههایی صعودی و در چه بازههایی نزولی است، این تابع در سراسر دامنه خود پیوسته و مشتق پذیر است، دارای دو نقطه بحرانی و یک نقطه عطف است.
زوج مرتب ((x,f(x) که نماینده نقطهای در صفحه دکارتی است را رسم میکنیم و به این ترتیب نمودار تابع f حاصل میشود. رسم نمودار تابع، باعث میشود دیدی کلی نسبت به آن تابع پیدا کنیم و همچنین بسیاری از خواص مربوط به توابع بویژه توابع حقیقی، مانند پیوستگی، مشتق پذیری، نقاط بحرانی و عطف، صعودی یا نزولی بودن و... از روی نمودار آنها قابل تعیین است. به عنوان مثال با بررسی شکل (۴) میتوان گفت این تابع در چه بازههایی صعودی و در چه بازههایی نزولی است، این تابع در سراسر دامنه خود پیوسته و مشتق پذیر است، دارای دو نقطه بحرانی و یک نقطه عطف است.
همچنین از روی نمودار یک رابطه میتوان تابع بودن آن را بررسی کرد. به عنوان مثال نمودار شکل (۱) معرف یک تابع نیست، زیرا عضو ۳ به دو مقدار متناظر شدهاست. همچنین در نمودار رسم شده در دستگاه دکارتی در شکل (۵)، برای هر عدد حقیقی مثبت x دو مقدار وجود دارد. به طور کلی یک نمودار در دستگاه مختصات دکارتی یک تابع است اگر هر خط عمودی مرسوم بر محور xها نمودار را حداکثر در یک نقطه قطع کند.
فضای توابع
اگر X و Y دو مجموعه باشند، مجموعه همه توابع از X به Y را با YX نشان میدهیم و بنابه تعریف داریم:
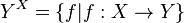
عدد اصلی این مجموعه را نیز میتوان به صورت زیر بدست آورد:
- card(YX) = (cardY)cardX
از رابطه فوق نتیجه میشود اگرX مجوعهای n-عضوی و Y مجموعهای m-عضوی باشد، تعداد توابع قابل تعریف از مجوعه X به مجموعه Y برابر است با mn که البته برای اثبات این مسئله خاص راه حل ترکیباتی هم وجود دارد. توضیح اینکه اگر بخواهیم تابع 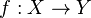 را تعریف کنیم هر عضو از n عضو مجموعهX چون
را تعریف کنیم هر عضو از n عضو مجموعهX چون  ، را میتوان به m طریق به یک عضو از مجموعه Y نسبت داد. پس بنابر اصل شمارش تعریف چنین تابعی به mn طریق ممکن خواهد بود.
، را میتوان به m طریق به یک عضو از مجموعه Y نسبت داد. پس بنابر اصل شمارش تعریف چنین تابعی به mn طریق ممکن خواهد بود.
توابع دو (یا چند) متغیره
عباراتی چون f(x,y) = sin(xy) یا f(x,y,z) = x2 + y2 + z2 را در نظر بگیرید. هر یک از آنها دو یا بیش از دو متغیر از دامنه میپذیرند و یک مقدار یگانه را به آنها نسبت میدهند. گاهی ممکن است تابع بجای یک شناسه دو یا چند شناسه را بپذیرد و آنها را به یک عضو از برد خود نسبت دهد، در این صورت تابع را دو یا چند متغیره میگوییم. چنین توابعی رابطهای بین بیش از دو مجموعه هستند. به عنوان مثال تابع اول را میتوان تابعی به صورت 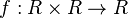 توصیف کرد که در این صورت تابع زوج (x,y) را به عنوان شناسه خود میپذیرد و آن را به عضوی از R نسبت میدهد که در این صورت اعضای تابع f را میتوان به صورت سه تایی ((x,y,f(x,y) نشان داد.
توصیف کرد که در این صورت تابع زوج (x,y) را به عنوان شناسه خود میپذیرد و آن را به عضوی از R نسبت میدهد که در این صورت اعضای تابع f را میتوان به صورت سه تایی ((x,y,f(x,y) نشان داد.
انواع تابع
توابع چندجملهای
توابع مثلثاتی
توابع مثلثاتی، تابعهایی هستند که زاویه را به نسبت طول اضلاع آن زاویه در یک مثلث قائمالزاویه مرتبط میکنند. توابع سینوس و کسینوس از جملهی مهمترین این توابع به شمار میروند. توابع مثلثاتی اهمیت بسیاری در ریاضیات کاربردی دارند و به خاطر ماهیت تناوبیشان، میتوانند بسیاری از پدیدههای تکرارشونده را توصیف کنند.
توابع متناوب
تابع همانی ( y=x )
تابع قدر مطلق
تابع ثابت (یعنی به ازای هر x ورودی y ثابت است.)
تابع پوشا